LAS FUNCIONES TRIGONOMÉTRICAS PARA ÁNGULOS DE 15°

Las funciones trigonométricas y los triángulos notables 

El primer paso que se hace necesario dar antes de entrar a establecer el significado del término razones trigonométricas es determinar el origen etimológico de las dos palabras que le dan forma:

-Razones deriva del latín, de “ratio”, que es sinónimo de “razón”.
-Trigonométrico, por su parte, tiene un origen griego. Significa “relativo a la trigonometría”, y está compuesta de los siguientes elementos de esa lengua: el sustantivo “trigonon”, que puede traducirse como “triángulo”; el nombre “metron”, que equivale a “medida”, y el sufijo “-ico”, que significa “relativo a”.

Trigonometría es el nombre de la rama de la matemática que se dedica realizar cálculos vinculados a los elementos de un triángulo.

Para esto trabaja con unidades como el grado sexagesimal (que se emplea al dividir una circunferencia en 360 grados sexagesimales), el radián (que se toma como la unidad natural de los ángulos y señala que la circunferencia es susceptible de división en 2 pi radianes).

\sqrt{\frac{2m+3}{2+\sqrt{2}}}

\sqrt[2]{\frac{3x+2}{6ab}}

$${\sqrt[2]{\frac{3x+2}{6ab}}}$$

LOS NÚMEROS FRACCIONARIOS OPERACIONES Y SUS REPRESENTACIONES

LOS NÚMEROS RACIONALES 

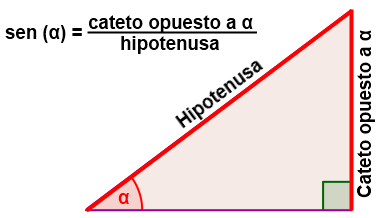
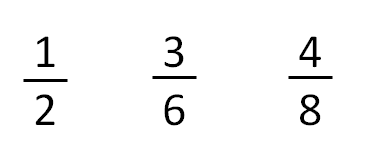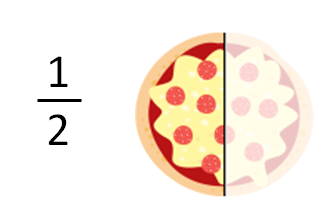Introducción 

Los egipcios calculaban la resolución de problemas prácticos utilizando fracciones cuyos denominadores son enteros positivos; son los primeros números racionales utilizados para representar las «partes de un entero», por medio del concepto de recíproco de un número entero.

Los matemáticos de la antigua Grecia consideraban que dos magnitudes eran conmensurables si era posible encontrar una tercera tal que las dos primeras fueran múltiplos de la última, es decir, era posible encontrar una unidad común para la que las dos magnitudes tuvieran una medida entera. El principio pitagórico de que todo número es un cociente de enteros, expresaba en esta forma que cualesquiera dos magnitudes deben ser conmensurables, luego números racionales. 

En las matemáticas, una fracción o un número fraccionario, (Proviene del vocablo latín frāctus, fractĭo -ōnis, roto, o quebrado)  es la expresión de una cantidad dividida entre otra cantidad; es decir que representa un cociente no efectuado de números. Por razones históricas también se les llama fracción común, fracción mixta o fracción decimal. 

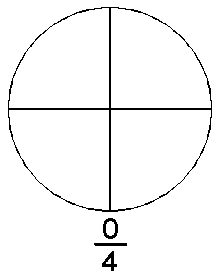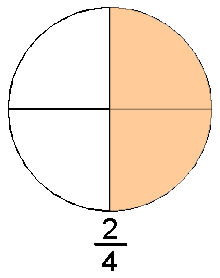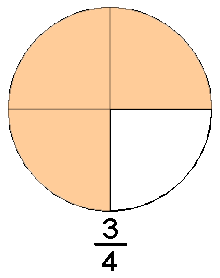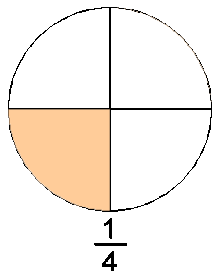
Todas las fracciones comunes se componen de: numerador, denominador y línea divisora entre ambos (barra horizontal u oblicua). 

En una fracción común ${\displaystyle a/b}$ el denominador "b" expresa la cantidad de partes iguales que representan la unidad, y el numerador "a" indica cuántas de ellas se toman.

El conjunto matemático que contiene a las fracciones de la forma a/b, donde a y b son números enteros y b≠0 es el conjunto de los números racionales, denotado como ℚ.

 En otras palabras, un número racional tiene la forma

Con b diferente de cero  donde  y  son números enteros.

Fracción simple o común

Una fracción simple (también conocida como fracción común o fracción vulgar) es un número racional de la forma a/b, donde a y b son números enteros y b≠0. Puesto que una fracción común representa un número racional.

Ejemplo 1

El número  fraccionario 1/4 se lee un cuarto. 

El denominador (4) Indica que se deben dibujar cuatro partes o son las partes en las que se debe dividir la unidad. 

El numerador (1). Indican que se debe tomar solo una parte de la unidad conformada por 4

_______________________________________________________________________

Ejemplo 2

El número  fraccionario 3/4 se lee tres cuartos.

El denominador (4) Indica que se deben dibujar cuatro partes o son las partes en las que se debe dividir la unidad.

El numerador (3). Indican que se deben tomar tres partes de la unidad conformada por 4

____________________________________________________________________

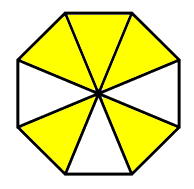Ejemplo 3

  ·         La unidad está dividida en 8 partes iguales.

  ·         Se han coloreado de amarillo 6 partes, es decir que las             mismas se tomaron de la unidad.

  ·         Por tanto el fraccionario es seis octavos 6/8 

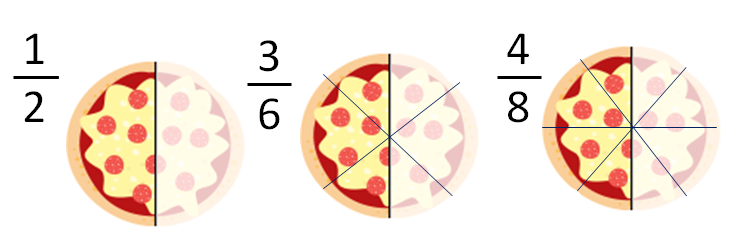
Las fracciones equivalentes son aquellas fracciones que representan una misma cantidad. Por ejemplo, las siguientes fracciones representan la misma cantidad al representarlas

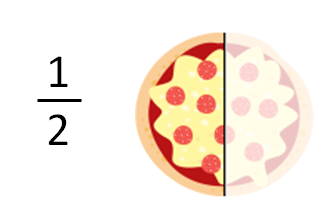
Se ha dibujado una pizza para representar 1/2, partiremos la pizza en 2 trozos y nos quedaremos con 1 trozo:

Para representar los 3/6, partiremos la pizza en 6 trozos iguales  y nos quedaremos con solo 3 trozos:

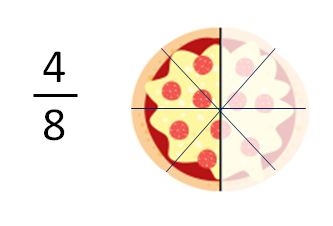
En la representación de los  4/8, partiremos la pizza en 8 trozos iguales  y nos quedaremos con 4 trozos:

Las tres fracciones representan la misma cantidad de pizza, justo la mitad, por eso se les llaman fracciones equivalentes.

___________________________________________________

      
      Una fracción propia es aquella en la que, si el numerador y el denominador son positivos, el  numerador es menor que el denominador, por ejemplo ${\displaystyle {\tfrac {1}{3}},\;{\tfrac {3}{8}},\;{\tfrac {3}{4}}}$

      Una fracción impropia es la fracción en donde el numerador es mayor que el denominador, por ejemplo 

Actividad 2

Consulta  a través de libros o la web los siguientes conceptos.

· ¿Qué es un fraccionario?

· ¿Qué es y qué significado tiene el numerador de una fracción?

· ¿Qué es y qué significado tiene el denominador de una fracción?

· ¿Qué es una fracción propia? Escribir y dibujar 4 ejemplos.

· ¿Qué es una fracción equivalente? Escribir y dibujar 4 ejemplos

· ¿Qué es una fracción impropia? Escribir y dibujar 4 ejemplos.

· ¿Qué es una fracción homogénea? Escribir y dibujar 4 ejemplos.

· ¿Qué es una fracción heterogénea? Escribir y dibujar 4 ejemplos

Actividades entregadas por el Grado 701

1 ALVAREZ YABISMAY TALIANA ANDREA  Geometría

2 ALVEAR PASTRANA MARIA ALEJANDRA  Geometría

3 ARIAS GARCIA MATIAS ESTEBAN  Geometría

4 BARRERA PARGA ROBINSON ANDRES  Geometría

5 BARRERA TORRES JULIAN FELIPE  Geometría

6 CASALLAS ARISMENDI MERY SCARLETT   Geometría

7 CASTILLOS AGUIAR YINESKHA DEL CARMEN  Geometría

8 CASTRO RAMIREZ JHON DAVID  Geometría

9 CUBIDES LATORRE LUIS ALEJANDRO  Geometría

10 DIAZ ALBADAN DIEGO CAMILO  Geometría

11 DUCUARA BAZURDO MARIA FERNANDA  Geometría

12 ESTRADA NIETO LAURA CHARIT  Geometría

13 GAITAN BARRERA BREINER ESTEBAN  Geometría

14 GARCIA GUACANEME JOSE DANIEL   Geometría

15 GARZON RODRIGUEZ JEIMY LUCERO   Geometría

16 GUTIERREZ RODRIGUEZ MARIA JOSE   Geometría

17 GUZMAN BRITO CAMILO ANDRES   Geometría

18 GUZMAN SARMIENTO WILLIAM  Geometría

19 HERNANDEZ LLANO JOSE ALEJANDRO  Geometría

20 LOSADA ACERO MAIKER JULIAN   Geometría

21 MARTIN LINARES JUAN PABLO  Geometría

22 MEJIAS RAMIREZ ROXELIS ALEJANDRA  Geometría

23 MENDEZ QUISHPE WILKA HALIL  Geometría

24 MENDIETA LONDOÑO NICOLE    Geometría

25 MENDIETA ROA ANGIE YULIETH   Geometría

26 MORENO ARIAS WENDY TATIANA   Geometría

27 NOVOA GUZMAN JHULEIDY KATHERINE   Geometría

28 PARDO MURILLO SERGIO ANDRES    Geometría

29 PARRADO BARONA JOAN SANTIAGO   Geometría

30 PRIETO BERMUDEZ JUAN JOSE   Geometría

31 QUEVEDO RIOS SHAROL YILANI   Geometría

32 RAMIREZ ROMERO LOREN JULIANA   Geometría

33 RAMIREZ VELASQUEZ JUAN DAVID   Geometría

34 RAMIREZ VERGAÑO YENCCY KARINA   Geometría

35 RAMOS ZEMA JONNY ALEXANDER    Geometría

36 SALAZAR VALENCIA LUIS ALEJANDRO   Geometría

37 URQUINA SERRATO VALERIA LISETH   Geometría

38 VELASQUEZ ADAN JUAN DIEGO    Geometría

39 YRIGOYEN GALINDEZ WEIDER ENRIQUE   Geometría

Actividades entregadas por el Grado 702

Actividades entregadas por el Grado 703

LAS RAZONES TRIGONOMÉTRICAS

Historia de las matemáticas en Egipto

La figura que se presenta en el papiro es la de un triángulo rectángulo donde la altura coincide con la longitud de uno de los catetos. Ello ha hecho proponer la posibilidad de que el cálculo, en vez del correcto que hemos apuntado, fuera erróneo debido a que tomarían por altura uno de los lados de forma general. En favor de esta hipótesis está el hecho de que la dimensión de la altura se coloca fuera de la figura triangular siendo la altura, sin embargo, un segmento fundamentalmente interior. Por otra parte, también se afirma que el término myrt  no es el usual para describir la altura, ya que cuando se calcula el volumen de un granero la altura recibe el nombre de kew.
   Sin embargo, esta ingeniosa hipótesis parece improbable debido a que, como se ha comprobado en otros papiros, el escriba egipcio reservaba el interior de las figuras únicamente para expresar su superficie con lo que no cabría colocar ahí el valor de la altura. Por otro lado, la altura kew de un granero tiene un sentido físico del que carece la altura myrt de una figura plana, por lo que tiene sentido que el escriba las distinguiera por escrito.

Desde el punto de vista matemático, es más interesante resaltar el hecho de que el procedimiento para el cálculo de la superficie de un triángulo se apoya en el más básico del área del rectángulo, 'transformando' el triángulo en un rectángulo. Esto cabe hacerlo de dos formas en un triángulo no rectángulo: Bien conservando la misma base y altura (con lo que el rectángulo resultante es de área doble que el triángulo), bien construyendo el rectángulo de la misma altura sobre la mitad de la base. Este segundo es un procedimiento más sencillo por cuanto utiliza la superficie que hay (lo que quita de un lado lo pone en el otro) en vez de construir una superficie auxiliar que luego hay que partir por la mitad. Además, la expresión 'completar el rectángulo' a partir de la mitad de la base, como realiza el problema, apunta en la misma dirección

Definiciones  de  trigonometría  y  relaciones  trigonométricas.

La trigonometría estudia a los triángulos, y las relaciones existentes que hay entre sus elementos, así como las aplicaciones que éstas tienen en la práctica, como la topografía, la astronomía, etc.

Etimológicamente, la palabra trigonometría significa  medida de triángulo, es decir, el cálculo del valor  de algún o algunos de sus  elementos.  De donde podemos definirla de la siguiente manera.

Las razones trigonométricas de un ángulo (α) letra griega llamada alfa, son las razones obtenidas entre los tres lados catetos e hipotenusa de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c.

Sen(α)

Se conoce a la  razón Seno de un ángulo (α) al valor, de la medida del segmento llamado cateto opuesto al ángulo α y la medida de la hipotenusa la llamaremos seno de α:

Cos(α)

Se conoce a la  razón Coseno de un ángulo (α) al valor, de la medida del segmento llamado cateto adyacente al ángulo α y la medida de la hipotenusa; a esta razón  la llamaremos Coseno de α:

Tan(α)

Se conoce a la  razón Tangente de un ángulo (α) al valor,de la medida del segmento llamado cateto opuesto al ángulo α y la medida del cateto adyacente; a esta razón la  llamaremos Tangente de α:

Las razones trigonométricas seno, coseno y tangente son las razones trigonométricas fundamentales; sin embargo, también se definen los valores recíprocos de ellas como las razones trigonométricas recíprocas.

Cot(α)

Se conoce a la  razón Cotangente de un ángulo a la inversa de la razón  tangente (α) al valor, de la medida del segmento llamado cateto adyacente al ángulo α y la medida del cateto opuesto; a esta razón la  llamaremos Cotangente de α:

Sec(α)

Se conoce a la  razón Secante de un ángulo a la inversa de la razón  Coseno (α) al valor, de la medida del segmento llamado hipotenusa al ángulo α y la medida del cateto adyacente; a esta razón la  llamaremos Secante de α:

Csc(α)

Se conoce a la  razón Cosecante de un ángulo a la inversa de la razón  Seno (α) al valor, de la medida del segmento llamado hipotenusa al ángulo α y la medida del cateto opuesto; a esta razón la  llamaremos Cosecante de α: