Sin embargo, esta ingeniosa hipótesis parece improbable debido a que, como se ha comprobado en otros papiros, el escriba egipcio reservaba el interior de las figuras únicamente para expresar su superficie con lo que no cabría colocar ahí el valor de la altura. Por otro lado, la altura kew de un granero tiene un sentido físico del que carece la altura myrt de una figura plana, por lo que tiene sentido que el escriba las distinguiera por escrito.
Desde el punto de vista
matemático, es más interesante resaltar el hecho de que el procedimiento para
el cálculo de la superficie de un triángulo se apoya en el más básico del área
del rectángulo, 'transformando' el triángulo en un rectángulo. Esto cabe hacerlo
de dos formas en un triángulo no rectángulo: Bien conservando la misma base y
altura (con lo que el rectángulo resultante es de área doble que el triángulo),
bien construyendo el rectángulo de la misma altura sobre la mitad de la base.
Este segundo es un procedimiento más sencillo por cuanto utiliza la superficie
que hay (lo que quita de un lado lo pone en el otro) en vez de construir una
superficie auxiliar que luego hay que partir por la mitad. Además, la expresión
'completar el rectángulo' a partir de la mitad de la base, como realiza el
problema, apunta en la misma dirección
Definiciones de trigonometría y relaciones trigonométricas.
La trigonometría estudia a los triángulos, y las relaciones existentes que hay entre sus elementos, así como las aplicaciones que éstas tienen en la práctica, como la topografía, la astronomía, etc.
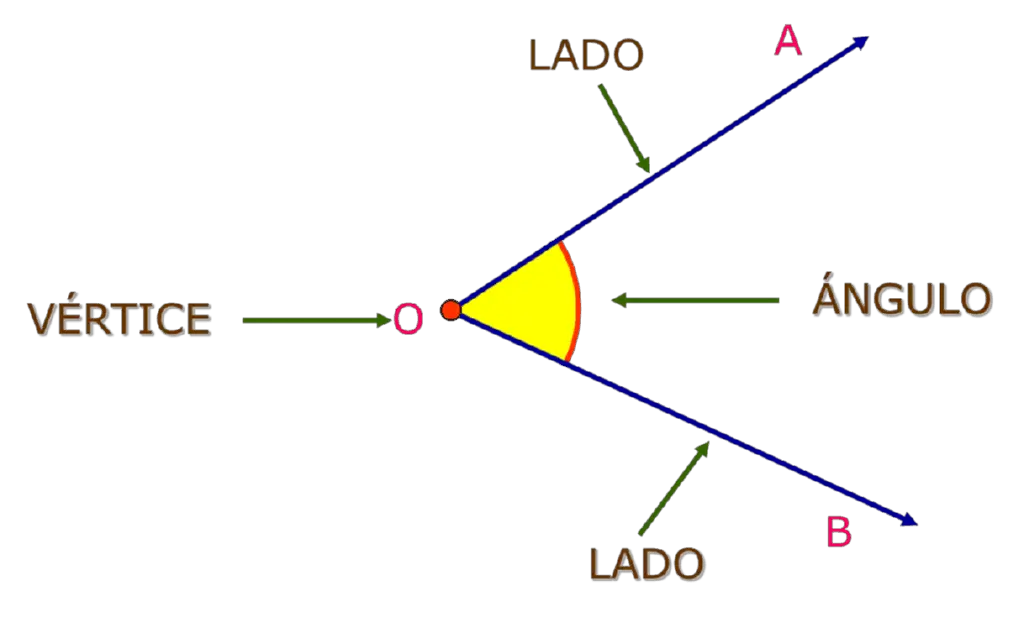
Etimológicamente, la palabra trigonometría significa medida de triángulo, es decir, el cálculo del valor de algún o algunos de sus elementos. De donde podemos definirla de la siguiente manera.
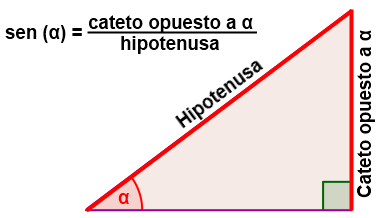
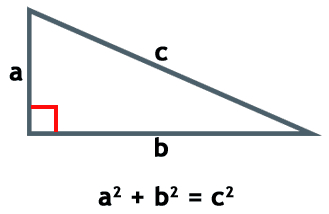
Las razones trigonométricas de un ángulo (α) letra griega llamada alfa, son las razones obtenidas entre los tres lados catetos e hipotenusa de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c.
Sen(α)
Cos(α)
Se conoce a la razón Coseno de un ángulo (α) al valor, de la medida del segmento llamado cateto adyacente al ángulo α y la medida de la hipotenusa; a esta razón la llamaremos Coseno de α:
Tan(α)
Se conoce a la razón Tangente de un ángulo (α) al valor,de la medida del segmento llamado cateto opuesto al ángulo α y la medida del cateto adyacente; a esta razón la llamaremos Tangente de α:
Las razones trigonométricas seno, coseno y tangente son las razones trigonométricas fundamentales; sin embargo, también se definen los valores recíprocos de ellas como las razones trigonométricas recíprocas.
Se conoce a la razón Cotangente de un ángulo a la inversa de la razón tangente (α) al valor, de la medida del segmento llamado cateto adyacente al ángulo α y la medida del cateto opuesto; a esta razón la llamaremos Cotangente de α:
