MEDIDAS DE ÁNGULOS Y EL CÍRCULO UNITARIO

 

INTRODUCCIÓN 

DEFINICIÓN DE ÁNGULO 

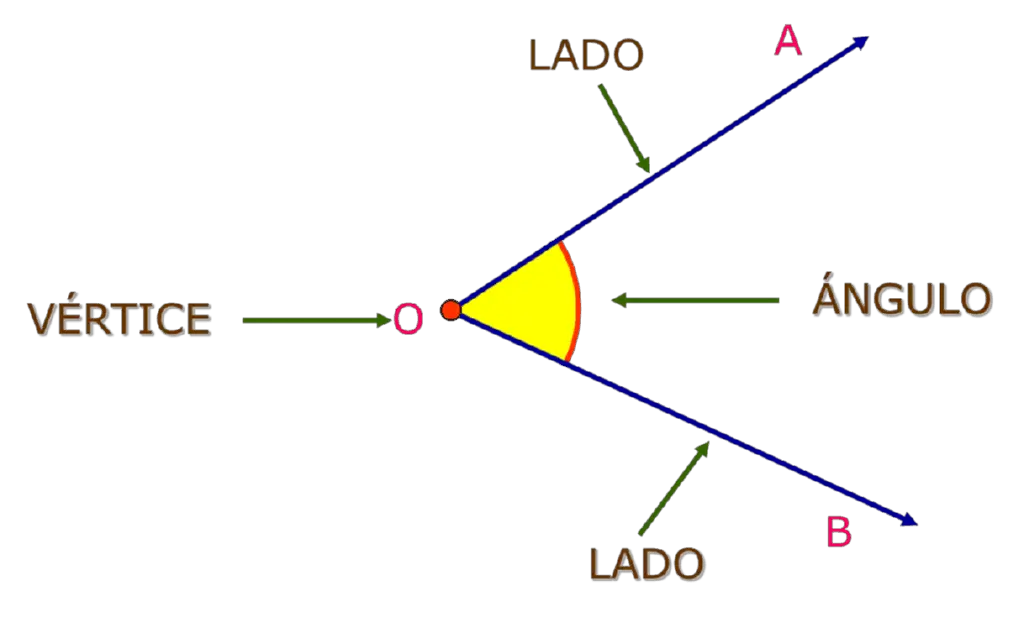Un ángulo en el plano se define como la abertura formada por dos semirrectas que tienen en común su origen, éstas se llaman lados del ángulo y el punto en común se denomina vértice.

A los lados del ángulo se les conoce como lado inicial y lado final, los cuales se determinan siguiendo el sentido contrario a las manecillas del reloj como se muestra en la figura, en cuyo caso decimos que el sentido es positivo, en caso contrario, el sentido sería negativo.

Los ángulos se pueden nombrar de diferentes formas, tomando en cuenta: 

Los puntos que se unen para formarlo.

La letra que distingue al vértice o bien por algún número asignado. 

_________________________________________________________________

MEDIDAS EN GRADOS Y RADIANES

Sistema de medida sexagesimal.

Aproximadamente en el año 1000 a.C. los babilonios extienden a los círculos celestes la división del día en 360 partes, y cada una de estas partes le llaman grado sexagesimal. y a la cuarta parte le corresponden 90 grados sexagesimales, que se nota por 90º.

Ahora bien como los babilonios utilizan el sistema de numeración de base 60, dividen el grado en 60 partes iguales y a cada una de estas partes la denomina minuto y se nota por 1'. Cada minuto lo subdividen a su vez en 60 segundos y cada una de estas subdivisiones lo notaron por 1''.

Así pues tenemos que un ángulo recto mide 90º, 1º= 60' y 1'= 60''.

Recordemos como se opera con grados sexagesimales.

Sistema de medida en radianes

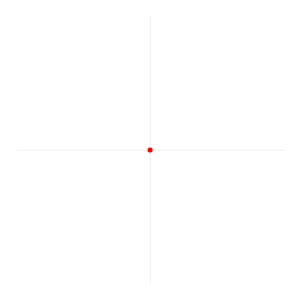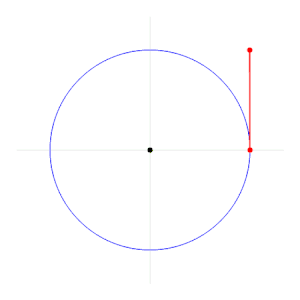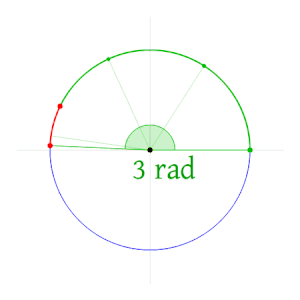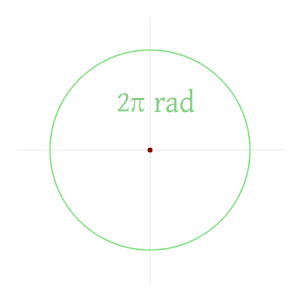Un radián (Dar clic) es el ángulo que se consigue cuando se toma el radio y se enrolla sobre el círculo. Veamos un dibujo para entenderlo mejor

                                                             (Dar clic sobre el cuadro)

_________________________________________________________________

CONVERSIÓN DE MEDIDAS EN GRADOS Y RADIANES

La relación entre grado sexagesimal y el sistema de medidas a través del radian, se representan por medio de las letras

R (radiandes) 

G (grados) sexagesimales 

están establecidas por la proporciones que se muestran en la imagen del lado izquierdo, lo cual se hace necesario para su comprensión mediante dos ejemplos ilustrativos de conversiones de medidas angulares.

Ejemplo 1: 

                  Transformar 45 grados a π radianes.

Solución:  45° x π radianes = π radianes

                      180°                    4

Ejemplo 2: 

Ejemplo 3: 

   

(Dar clic sobre la imagen)

Ejemplo 4:

                                       Convertir 60° y 45° a radianes

_________________________________________________________________

Círculo unitario de medidas de ángulos 

El círculo unitario es un círculo de radio 1 (por eso se llama unitario), y es una gran herramienta en trigonometría y geometría analítica ya que nos permite visualizar de manera rápida los ángulos en radianes o medidos en sistema sexagesimal, también los valores de las funciones seno y coseno de los ángulos. Además, se puede establecer la relación entre los 4 cuadrantes y los signos fácilmente.

A continuación se presenta un círculo unitario con las medidas de los ángulos en grados y radianes. Nótese la relación entre los ángulos del mismo color, ya que son las mismas cifras pero diferentes signos.

Circulo unitario para ángulos de 15 en 15 grados 

ACTIVIDAD

• Hallar las medidas en radianes para los siguientes ángulos. 15, 30, 45, 60, 75, 90....de  15 en 15, hasta 360°

• Determinar todas las medidas  en π/3 radianes hasta 14π/3. Es decir π/3, 2π/3, π, 4π/3.....hasta 14π/3. 

• Convertir 1320°, 730°, 850° a radianes.

• Convertir  350π / 7 , 56π/15 , 37π /2  y   56π / 2   a grados sexagesimales.