MATEMÁTICAS GRADOS 7° Y 10°: EL TEOREMA DE PITÁGORAS Y LA INTRODUCCIÓN A LA TRIGONOMETRÍA

TEOREMA DE PITÁGORAS

HISTORIA.
El teorema se le atribuye al filósofo y matemático griego Pitágoras, aunque no se sabe si es el autor efectivo. Se tienen pruebas que los babilonios poseían algún conocimiento del mismo (o al menos de enteros especiales conocidos como ternas pitagóricas que lo integran) al menos un milenio antes.

Del mismo modo, en el Zhoubi Suanjing (El clásico matemático de la sombra de Zhou), uno de los textos de matemática china más antiguos de la historia, y que fue escrito entre el 500 y 300 a.C, contiene una de las primeras pruebas escritas del teorema.

________________________________________________________________

RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS.

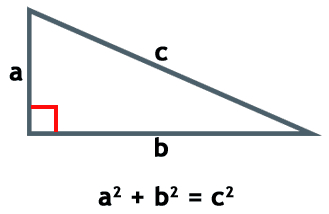
Si sabemos las longitudes de dos lados o la hipotenusa y un lado de un triángulo rectángulo, el teorema de Pitágoras nos ayudara a encontrar el tercer lado faltante. Dado un triangulo rectángulo de catetos (a) y (b) y de hipotenusa (h), entonces el cuadrado de la hipotenusa es igual a la suma del cuadrado de los catetos.

Ecuaciones de los lados(Dar Click)

Se le llama triángulo rectángulo, porque tiene un angulo recto, es decir que este mide 90°.

La hipotenusa es el lado más largo de un triángulo rectángulo.

La comprensión del teorema de Pitágoras es sencilla y tiene muchas aplicaciones en la vida cotidiana y es una de las herramientas aplicables en la trigonometría para la deducción de las razones trigonométricas en estudios posteriores.

EJEMPLO 1

Supongamos que queremos calcular la altura del extremo donde está apoyada la escalera en la pared, si esa escalera mide 5 metros y la distancia de la pared a la base de la escalera es de 3 metros. ¿A qué altura del piso está apoyada la escalera?

La resolución de este problema es muy simple, tenemos que hacer uso de la ecuación del teorema de Pitágoras, donde la incognita es uno de los catetos.

Solución

Por tanto la altura del piso a la pared es de 4 metros.

EJEMPLO 2

Hallar la altura (x) medida en metros de una nave que proyecta una sombra a 120 metros y la distancia de la punta de la misma hasta el anclaje es de 130 metros

Para ver la explicación

(Dar click sobre la imagen)

EJEMPLO 3

EJEMPLO 4

________________________________________________________________

Ejercicios

1. Hallar la hipotenusa de un triángulo rectángulo de catetos 5 cm y 12 cm.

2. Hallar el menor lado de un triángulo rectángulo si los otros dos lados miden 8 cm y 10 cm.

3. Calcular la hipotenusa de un triángulo rectángulo si los catetos miden 1 cm y 2 cm.

4. Determina el valor de los catetos (x) y (2x) según los datos de la figura.

5. Hallar el valor de x de los catetos según el diagrama

6 Determina el valor de la variable (x) en el cateto para este caso.

7. ¿Cuál sería el valor correspondiente para cateto compartido por los triángulos y la incógnita (x)?

8. Calcular el área de una superficie rectangular si su diagonal mide 25 cm y su base 24 cm.

9. Calcular el área de de una superficie rectangular si su diagonal mide 15 cm y su altura 9 cm

10. ¿Qué valor tendría la expresión en el caso de x² – 6, al despejar la incógnita (x) del triángulo?

_____________________________________________________________

DISTANCIA ENTRE DOS PUNTOS

Definición

¿Qué es la distancia entre dos puntos sobre un plano? Es simplemente la distancia mínima que hay entre ambas posiciones, las cuales vienen determinadas por las sus coordenadas en el eje de las X y en el eje de las Y.

distancia entre dos puntos en el plano cartesiano

El teorema de Pitágoras se puede usar para calcular la distancia entre dos puntos o la línea recta que separan los puntos (P) y (Q) en un plano cartesiano. Dados dos puntos en el plano.

Ejemplo 1

P_1(7,

¿Cuál es la distancia mínima sobre el plano cartesiano que separa los siguientes dos puntos? P₁ (2, 1) y P₂ (4, 5)

(Dar click sobre la imagen)

______________________________________________________________

ACTIVIDAD

Aplica los conceptos adquiridos para la resolución de los problemas del cuadernillo desde el ejercicio 5 hasta el 96.

(Dar click sobre la imagen)

El estudiante debe registrar evidencia de todos los procedimientos necesarios para la resolución del cuaderno de ejercicios, los cuales tienen que ver con el calculo de las raíces cuadradas.

(Dar click sobre la imagen)